Room allocation problem
The problem described here has been
inspired
by the Sisyphus I problem. The goal is to
assign a
group
of people to available rooms. The people, who have to be
assigned,
are characterised by their features. A set of rooms is described
by another set of attributes. The problem is to allocate these
people within available rooms in such a way that the allocation
meets the criteria for the required functionality of the group
of
people as a whole.
For the illustration of this problem let us consider personnel
of a
research team. Individuals (members of the team) differ from one
another by their position within the team hierarchy, projects
they
participate on, and their attitude to smoking and computers. The
group consists of fifteen people:
| name | position | project
| smoker | hacker |
| thomas | head-of-group | mlt |
| |
| hans | head-of-project | babylon |
yes | |
| katharina | head-of-project | mlt |
yes | yes |
| joachim | head-of-project | aserti |
| |
| werner | researcher | babylon |
| yes |
| angi | researcher | babylon |
| |
| harry | researcher | babylon |
| yes |
| jurgen | researcher | mlt |
| yes |
| marc | researcher | aserti |
| |
| uwe | researcher | mlt |
yes | yes |
| andy | researcher | mlt |
yes | |
| michael | researcher | mlt |
| yes |
| monika | secretary | |
| |
| ulrike | secretary | |
| |
| eva | manager | |
| |
These persons have to be assigned to new rooms according to
the following figure:
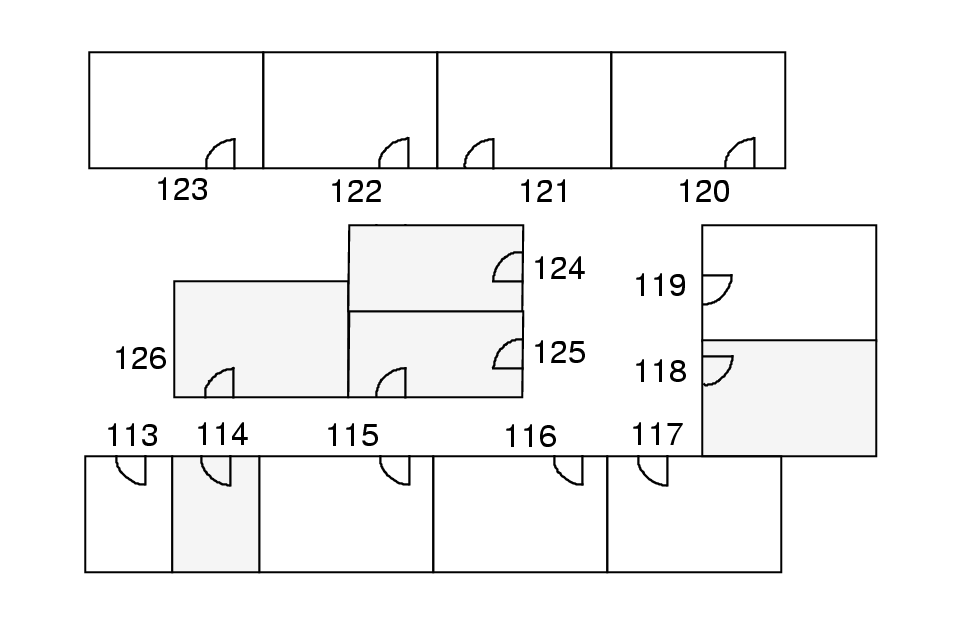
Rooms of different sizes are available. Let us consider only two
types of rooms - small rooms (113, 114, 124, and 125) and large
rooms. Only one person can be assigned to a small room. In a
large
room two persons can be llocated simultaneously. Marked rooms
(114,
118, 124, 125, and 126) are not available - they cannot be
used. Rooms 115, 116, 117, 118, 119, 124 and
125
are central.
The fact that only one person is allowed to be assigned to a
small room and maximum two person to a large one can be expressed
in the form of two constraints:
-
general1:
(all x y v)
-
(anybody(x) & in-room(x v) & anybody(y) & in-room(y v)
==> eq(x y))
-
general2:
(all x y z v)
-
(anybody(x) & in-room(x v) & anybody(y) & in-room(y v)
& anybody(z) & in-room(z v)
==> eq(x y) v eq(x z) v eq(y z))
These two constraints hold for any person. The other constraints
are relevant only for a group of people (there are separate sets
of constraints for people of different position within the
hierarchy):
HEAD-OF-GROUP
Head-of-group can be allocated in a large central room. At the
same time, he cannot share this room with anybody else.
-
head-of-group1:
(all x y)
-
(head-of-group(x) & in-room(x y)
==> central(y))
-
head-of-group2:
(all x y)
-
(head-of-group(x) & in-room(x y)
==> large(y))
-
head-of-group3:
(all x y z)
-
(head-of-group(x) & in-room(x z) & anybody(y) & in-room(y z)
==> eq(x y))
SECRETARIES
They share a large room close to the room of the head-of-group.
-
sec1:
(all x y)
-
(secretary(x) & in-room(x y)
==> large(y))
-
sec2:
(all x y v w)
-
(secretary(x) & secretary(y) & not eq(x y)
& in-room(x v) & in-room(y w)
==> eq(v w))
-
sec3:
(all x y v w)
-
(secretary(x) & in-room(x v) & head-of-group(y)
& in-room(y w)
==> close(v w))
MANAGER
Her office should be large and central. Moreover, her room has to
be as close as possible (to have maximum access to) to the
head-of-group and secretariat. She cannot share her room.
-
man1:
(all x y)
-
(manager(x) & in-room(x y)
==> central(y))
-
man2:
(all x y)
-
(manager(x) & in-room(x y)
==> large(y))
-
man3:
(all x y z v p q)
-
(manager(x) & in-room(x v) & head-of-group(y) & in-room(y p)
& secretary(z) & in-room(z q)
==> maximum-access(v p q))
-
man4:
(all x y z)
-
(manager(x) & in-room(x z) & anybody(y) & in-room(y z)
==> eq(x y))
HEAD-OF-PROJECTS
Preferably they do not share the room but they can share the room with the
person of the same position. The room of a head-of-project is
small (if it is possible).
-
head-of-project1:
(all x y)
-
(head-of-project(x) & in-room(x y)
==> small(y))
-
head-of-project2:
(all x y z)
-
(head-of-project(x) & in-room(x z) & anybody(y) & in-room(y z)
==> eq(x y))
-
head-of-project3:
(all x y v)
-
(head-of-project(x) & in-room(x v) & anybody(y)
& in-room(y v) & not eq(x y)
==> head-of-project(y))
RESEARCHERS
Smokers and non-smokers should be in different rooms. Two
researchers can share the room if both of them work on the same
project and only one of them is a hacker.
-
res1:
(all x y z v w)
-
(researcher(x) & researcher(y) & not eq(x y)
& in-room(x z) & in-room(y z) & smokes(x v) & smokes(y w)
==> eq(v w))
-
res2:
(all x y z v w)
-
(researcher(x) & researcher(y) & not eq(x y)
& in-room(x z) & in-room(y z) & project(x v) & project(y w)
==> eq(v w))
-
res3:
(all x y z v w)
-
(researcher(x) & researcher(y) & not eq(x y)
& in-room(x z) & in-room(y z) & hacker(x v) & hacker(y w)
==> not eq(v w))

