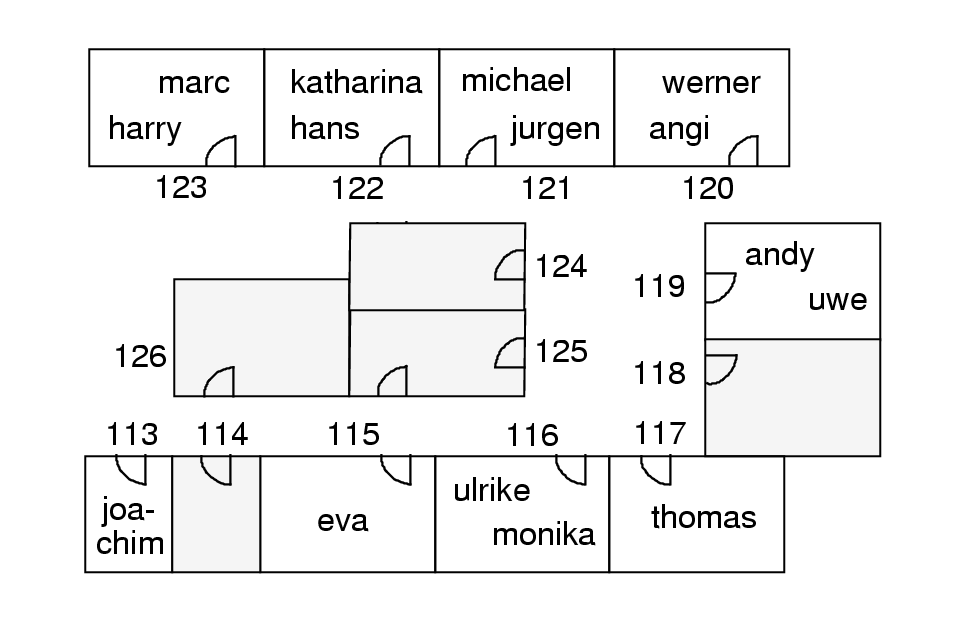
Example of solving RAP

Fifteen persons should be allocated to one small and eight large rooms. Altogether here are seventeen free positions in all available rooms. Thus the test for the solution existence succeeds and the search for the final solution can progress to the initialization task.

First, explicit initialization is done. Since only knowledge for the initialization of head-of-group and head-of-projects has been implemented, the explicit initialization can be done only for four parameters (representing thomas, hans, katharina, and joachim). Thomas can be assigned to a large central room. On the other hand, only one head-of-project can be initialized in such a way (e.g. hans), because only one small room is available. Parameters which stand for katharina and joachim cannot be initialized by the use of domain knowledge. These two parameters together with the others have to be initialized in an implicit way. The first values from the corresponding domain sets are assigned to these parameters. Since each person can be assigned to an arbitrary available room, the parameters have the same domain set. As a result of this, thirteen people are assigned to the same room.

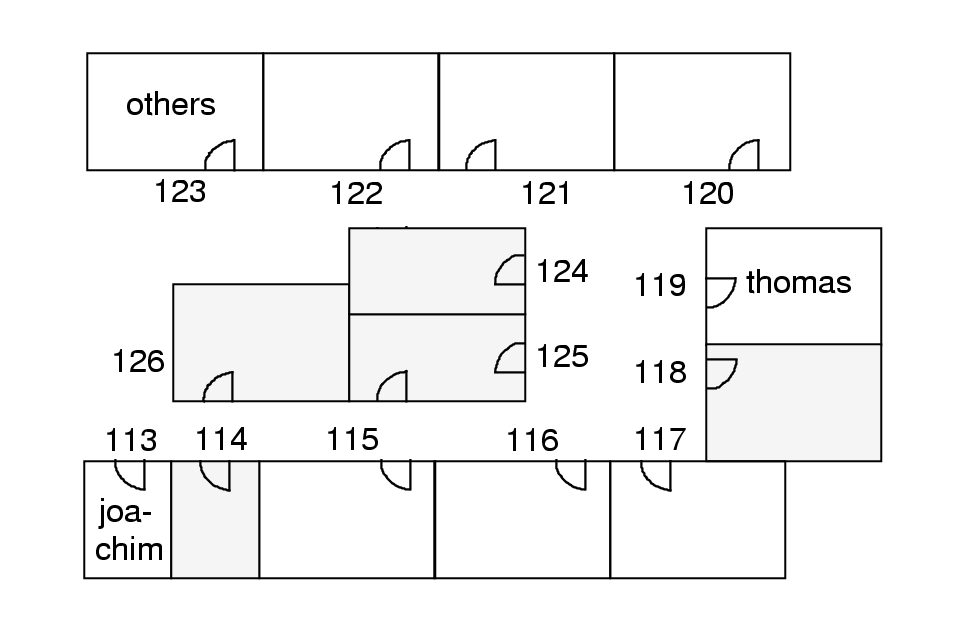
In this case not only the parameters concerning the required functionality of the final solution are violated but also the parameters which guarantee the solution to be physically possible (general1 and general2) are violated too.

general1: & active: yes & viol: no & ()
general2: & active: yes & viol: yes & (hans katharina werner angi harry jurgen marc uwe andy michael monika ulrike eva)

The constraint general2 (only two people can share a large room) is violated by thirteen parameters. For this reason the system moves the people from the room 123 into empty rooms until only two people remain in this room (and the constraint general2 holds). Now the solution has the form according this figure.

Although the present state of the solution represents a real applicable solution there are still some constraints violated. The state of the constraint violations is as follows:

head-of-group1: & active: yes & viol: no & ()
head-of-group2: & active: yes & viol: no & ()
head-of-group3: & active: yes & viol: yes & (thomas)
sec1: & active: yes & viol: no & ()
sec2: & active: yes & viol: yes & (ulrike monika)
sec3: & active: yes & viol: yes & (monika ulrike)
man1: & active: yes & viol: yes & (eva)
man2: & active: yes & viol: no & ()
man3: & active: yes & viol: yes & (eva)
man4: & active: yes & viol: yes & (eva)
head-of-project1: & active: yes & viol: yes & (hans katharina)
head-of-project2: & active: yes & viol: yes & (hans katharina)
head-of-project3: & active: no & viol: no & ()
res1: & active: yes & viol: no & ()
res2: & active: yes & viol: yes & (michael harry jurgen marc)
res3: & active: yes & viol: yes & (harry jurgen marc)
general1: & active: yes & viol: no & ()
general2: & active: yes & viol: no & ()

The constraint with the highest priority among violated constraints is the one concerning the head-of-group (this constraint was satisfied after the initialization step but became violated as a result of removing the violation of the constraint general2 with higher priority). For this reason marc is moved from 119 into the empty room 115:

The previous change results not only in fixing the violation of the constraint head-of-group3 but has another positive side-effect - marc does not violate the constraints res2 and res3 any more.

Now the violated constraints with the highest priority are those concerning secretaries. Two moves (the allocation both secretaries into the same large room and the replacement of the room which is allocated close to the head-of-group's room by the secretaries' room) generate the solution represented in the next figure.

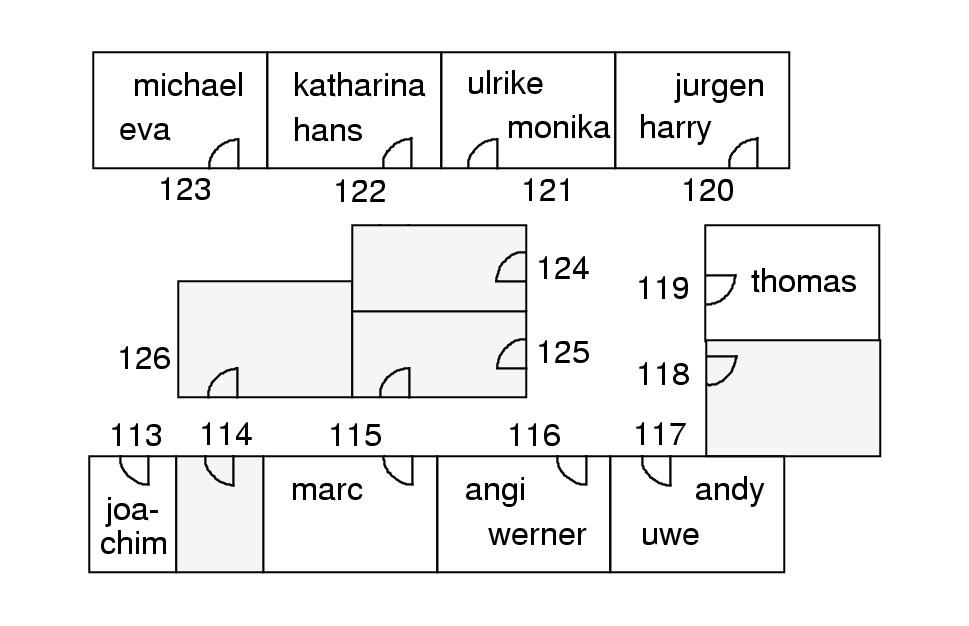
At this stage of the solution all constraints concerning secretaries hold. Since as a result of relocation of andy and uwe, the large central room is empty, the constraints concerning manager are no longer in a state of violation:

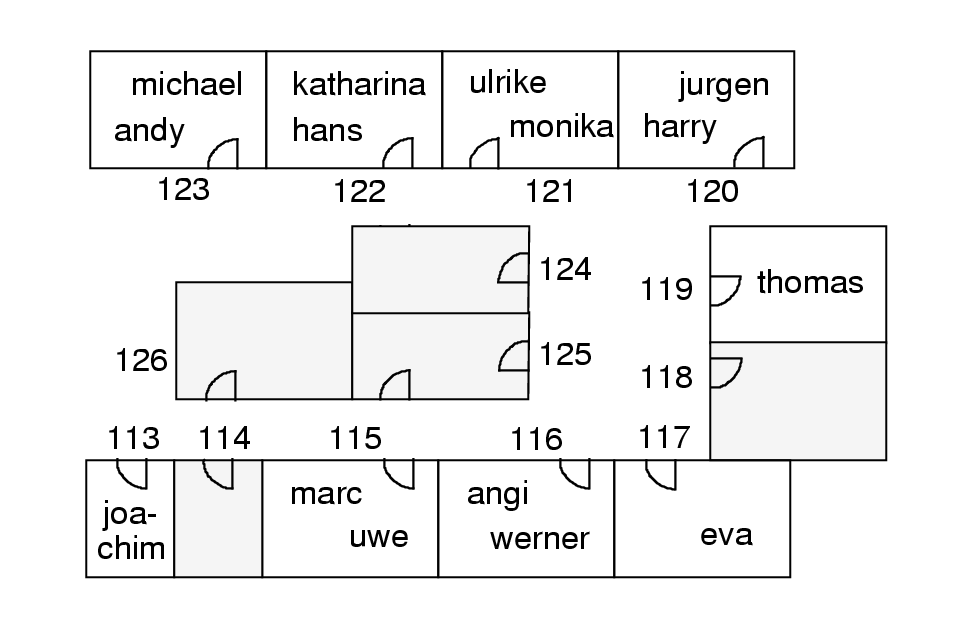
The present state of the constraints is as follows:

head-of-group1: & active: yes & viol: no & ()
head-of-group2: & active: yes & viol: no & ()
head-of-group3: & active: yes & viol: no & ()
sec1: & active: yes & viol: no & ()
sec2: & active: yes & viol: no & ()
sec3: & active: yes & viol: no & ()
man1: & active: yes & viol: no & ()
man2: & active: yes & viol: no & ()
man3: & active: yes & viol: no & ()
man4: & active: yes & viol: no & ()
head-of-project1: & active: yes & viol: yes & (hans katharina)
head-of-project2: & active: yes & viol: yes & (hans katharina)
head-of-project3: & active: no & viol: no & ()
res1: & active: yes & viol: yes & (marc uwe michael andy)
res2: & active: yes & viol: yes & (marc uwe harry jurgen)
res3: & active: yes & viol: yes & (harry jurgen)
general1: & active: yes & viol: no & ()
general2: & active: yes & viol: no & ()

It is not possible to ensure that each head-of-project occupies a small room (the constraint head-of-project1), because only one small room is available. Fortunately, the constraint head-of-project1 can be relaxed - it can be inactivated. The consequence of this inactivation is that head-of-project can be assigned to a large room. But there is not enough rooms to ensure that head-of-project does not share his/her room with anybody else. For this reason the constraint head-of-project2 should be inactivated too. Since now head-of-projects can share rooms, the constraint head-of-project3 has became meaningful and should be activated. By chance this constraint holds and there is no need to modify the allocation of people. The constraints are:

head-of-project1: & active: no & viol: no & ()
head-of-project2: & active: no & viol: no & ()
head-of-project3: & active: yes & viol: no & ()

All constraints concerning researchers are violated:

res1: & active: yes & viol: yes & (marc uwe michael andy)
res2: & active: yes & viol: yes & (marc uwe harry jurgen)
res3: & active: yes & viol: yes & (harry jurgen)

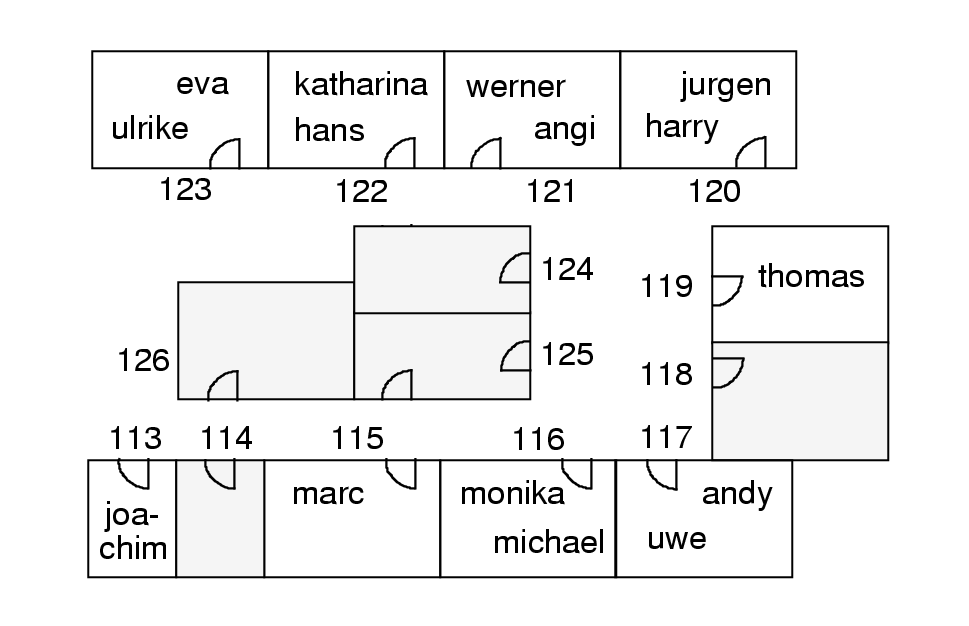
A few moves can produce the solution of the form depicted in the following figure.

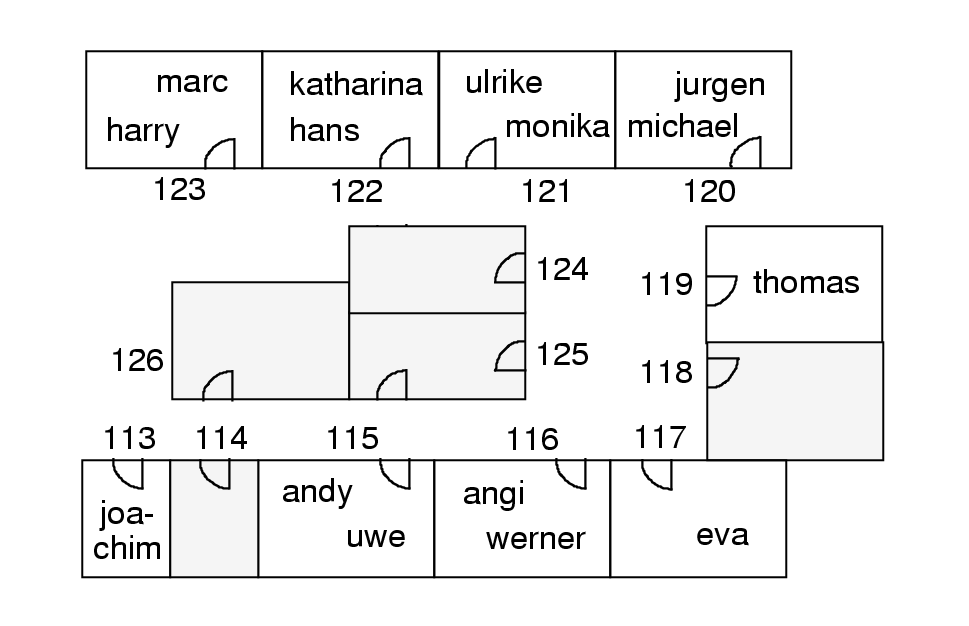
where the states of the constraints res1, res2, and res3 are:

res1: & active: yes & viol: no & ()
res2: & active: yes & viol: yes & (marc harry)
res3: & active: yes & viol: yes & (michael jurgen)

Different numbers of researchers working on different projects lead to the violation of res2 which cannot be removed. That is why this constraint should be relaxed. The same is true for the constraint res3.

Having done this, all active constraints hold and the search for the final solution of the room allocation problem moves from the task evaluate to the task optimize. Within this task rooms are swapped in order to optimize the terms `close' (the constraint sec3) and `maximum access' (the constraint man3). The final solution is depicted in the figure: